Kalman Tracking

The purpose of the Kalman filter is to estimate the state of a tracked vehicle. Here, "state" could include the position, velocity, acceleration or other properties of the vehicle being tracked. The Kalman filter uses measurements that are observed over time that contain noise or random variations and other inaccuracies, and produces values that tend to be closer to the true values of the measurements and their associated calculated values. It is the central algorithm to the majority of all modern radar tracking systems.

Here, we will be keeping the Kalman Filter limited to a basic introduction. You will be covering Kalman filters in detail in the fourth course of this Nanodegree program.

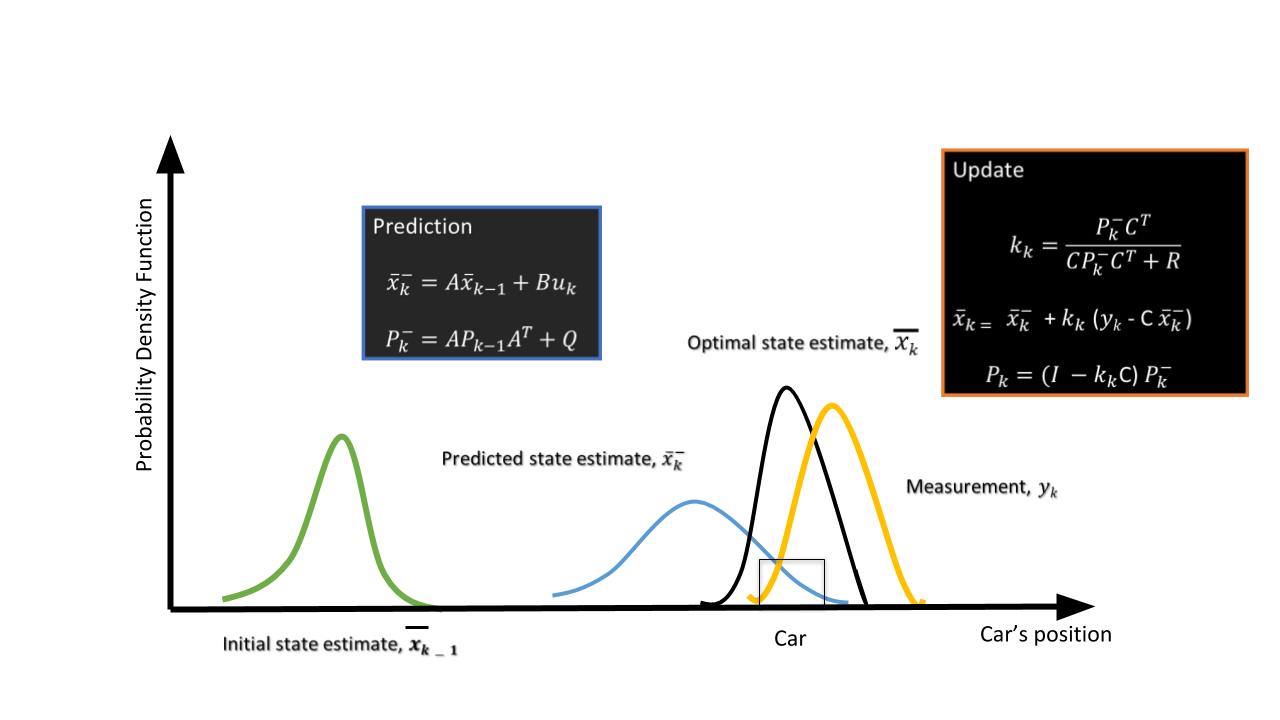
The Kalman filter process has two steps: prediction and update.

1. Prediction Step

   Using the target vehicle's motion model, the next state of the target vehicle is predicted by using the current state. Since we know the current position and velocity of the target from the previous timestamp, we can predict the position of the target for next timestamp.

   For example, using a constant velocity model, the new position of the target vehicle can be computed as:

2. Update Step :

   Here, the Kalman filter uses noisy measurement data from sensors, and combines the data with the prediction from the previous step to produce a best-possible estimate of the state.

Kalman Tracking and MATLAB

The trackingKF class creates a discrete-time linear Kalman filter used for tracking positions and velocities of objects which can be encountered in an automated driving scenario, such as automobiles, pedestrians, bicycles, and stationary structures or obstacles.

You can learn more about different parameters for the filter here , and you can learn more about the theory behind Kalman filters here .

Implementation in MATLAB

The following guidelines can be used to implement a basic Kalman filter for the next project.

• You will define the Kalman filter using the trackingKF function. The function signature is as follows:

       filter = trackingKF('MotionModel', model, 'State', state, 'MeasurementModel', measurementModel, 'StateCovariance', stateCovrariance, 'MeasurementNoise', measurementNoise)

In this function signature, each property (e.g. 'MotionModel ) is followed by the value for that property (e.g. model ).

• For the model variable, you can pass the string '2D Constant Velocity' , which will provides the 2D constant velocity motion model.
• For the 2D constant velocity model the state vector (x) can be defined as:

[x;vx;y;vy]

Here, x and y are 2D position coordinates. The variables vx and vy provide the velocity in 2D.

• A RadarDetectionGenerator function is used to generate detection points based on the returns after reflection. Every Radar detection generates a detection measurement and measurement noise matrix:
  detection.Measurement and detection.MeasurementNoise .The detection measurement vector (z) has the format [x;y;vx;vy] .

  Measurement Models

  Measurements are what you observe about your system. Measurements depend on the state vector but are not always the same as the state vector.The measurement model assumes that the actual measurement at any time is related to the current state by

z  = H*x

As a result, for the case above the measurement model is H = [1 0 0 0; 0 0 1 0; 0 1 0 0; 0 0 0 1]

Using this measurement model, the state can derived from the measurements.

 x = H'*z
state = H'*detection.Measurement

Further, using the generated measurement noise and measurement model define the state covariance matrix:

stateCovariance =H'*detection.MeasurementNoise*H

Further Research

For further explanation of Kalman Filters with MATLAB, you can refer to this video series .